递归

递归 是一种在函数内部调用同一函数的编程技术。尾递归 是一种可以显式应用于某些递归函数的优化技术。

递归函数使用前一个递归调用的结果。阶乘是一个常见的例子，factorial(n) 将从 1 到 n 的所有数字相乘，可以定义如下：

• factorial(1) 是 1
• factorial(n) 是 n * factorial(n - 1)

factorial() 是递归的，因为它使用来自相同函数应用于其修改后的参数的结果。这是 factorial() 的递归实现：

// Recursion/Factorial.kt
package recursion
import atomictest.eq

fun factorial(n: Long): Long {
  if (n <= 1) return 1
  return n * factorial(n - 1)
}

fun main() {
  factorial(5) eq 120
  factorial(17) eq 355687428096000
}

虽然这种方法易于阅读，但它的成本很高。在调用函数时，关于该函数及其参数的信息会存储在 调用栈 中。当抛出异常并且 Kotlin 显示 堆栈跟踪 时，您可以看到调用栈：

// Recursion/CallStack.kt
package recursion

fun illegalState() {
  // throw IllegalStateException()
}

fun fail() = illegalState()

fun main() {
  fail()
}

如果您取消注释包含异常的行，您将会看到以下内容：

Exception in thread "main" java.lang.IllegalStateException
  at recursion.CallStackKt.illegalState(CallStack.kt:5)
  at recursion.CallStackKt.fail(CallStack.kt:8)
  at recursion.CallStackKt.main(CallStack.kt:11)

堆栈跟踪显示在抛出异常时的调用栈状态。对于 CallStack.kt，调用栈仅由三个函数组成：

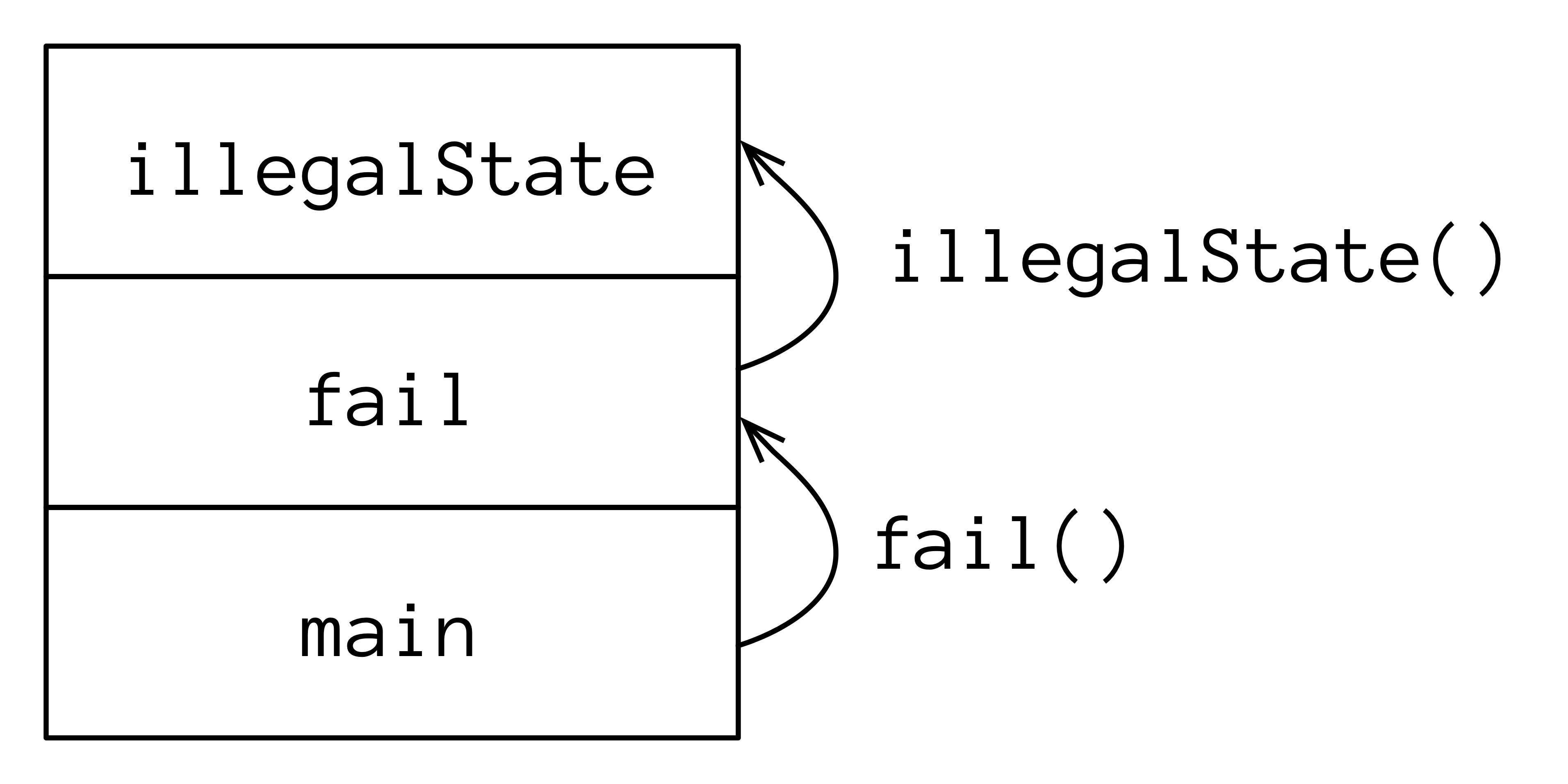
调用栈

我们从 main() 开始，它调用 fail()。fail() 调用将添加到调用栈中，以及它的参数。接下来，fail() 调用 illegalState()，也被添加到调用栈中。

当您调用递归函数时，每次递归调用都会向调用栈添加一个帧。这很容易导致 StackOverflowError，这意味着您的调用栈变得太大，耗尽了可用的内存。

程序员通常会因为忘记终止递归调用链而导致 StackOverflowError，这是 无限递归：

// Recursion/InfiniteRecursion.kt
package recursion

fun recurse(i: Int): Int = recurse(i + 1)

fun main() {
  // println(recurse(1))
}

如果您在 main() 中取消注释该行，您将会看到包含许多重复调用的堆栈跟踪：

Exception in thread "main" java.lang.StackOverflowError
at recursion.InfiniteRecursionKt.recurse(InfiniteRecursion.kt:4)
at recursion.InfiniteRecursionKt.recurse(InfiniteRecursion.kt:4)
...
at recursion.InfiniteRecursionKt.recurse(InfiniteRecursion.kt:4)

递归函数不断地调用自身（每次使用不同的参数），并填充调用栈：

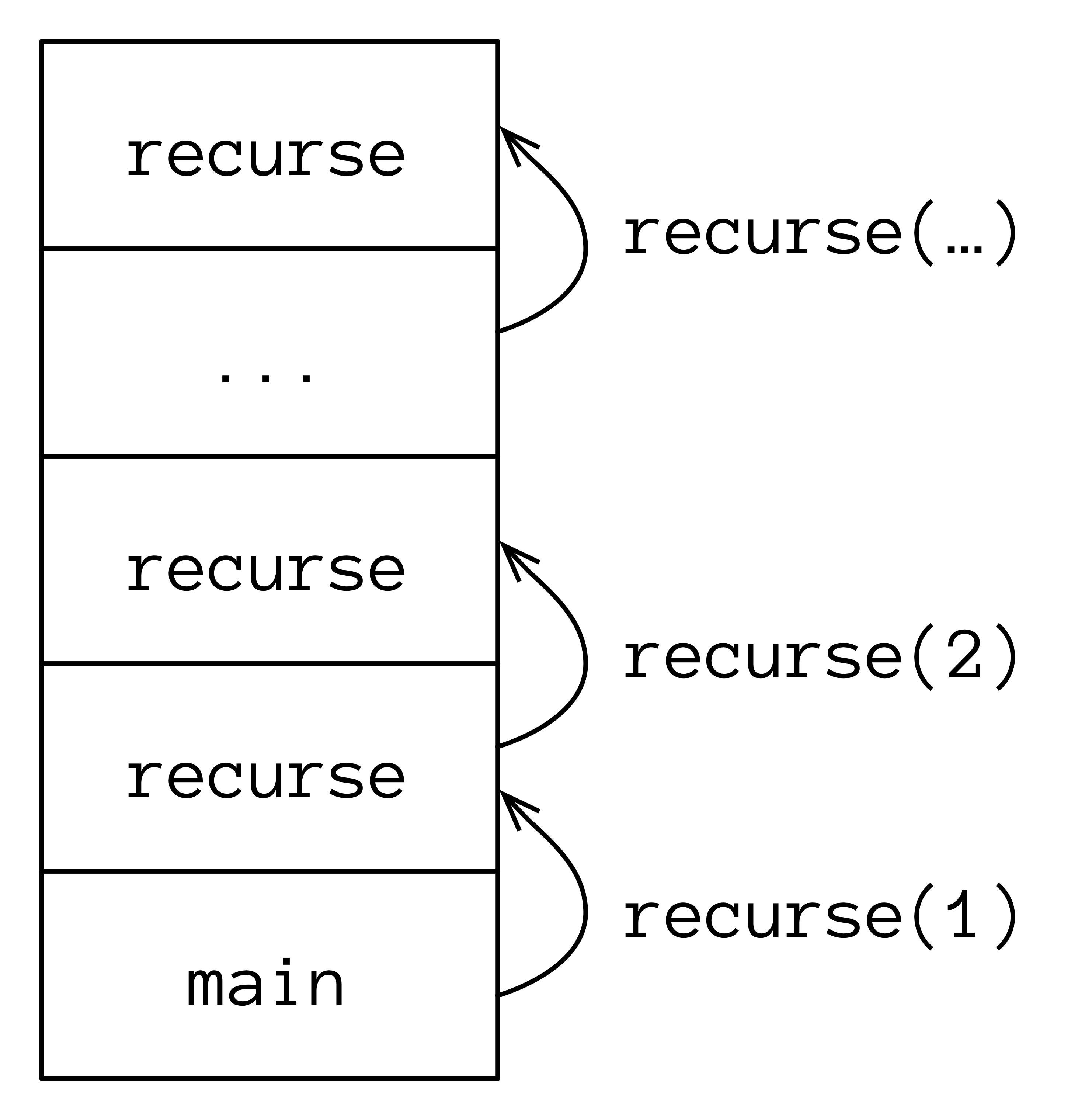
无限递归

无限递归总是以 StackOverflowError 结束，但您也可以通过调用足够多的递归函数调用来获得相同的结果。例如，让我们递归地计算到给定数字的整数之和，将 sum(n) 递归地定义为 n + sum(n - 1)：

// Recursion/RecursionLimits.kt
package recursion
import atomictest.eq

fun sum(n: Long): Long {
  if (n == 0L) return 0
  return n + sum(n - 1)
}

fun main() {
  sum(2) eq 3
  sum(1000) eq 500500
  // sum(100_000) eq 500050000       // [1]
  (1..100_000L).sum() eq 5000050000  // [2]
}

这种递归很快变得昂贵。如果您取消注释 **[1

]** 行，您会发现它花费太长时间来完成，所有这些递归调用会导致堆栈溢出。如果 sum(100_000) 在您的计算机上仍然可以工作，请尝试更大的数字。

调用 sum(100_000) 会导致 StackOverflowError，因为它将 100_000 个 sum() 函数调用添加到调用栈中。作为比较，[2] 行使用 sum() 库函数来添加范围内的数字，而这不会失败。

为了避免 StackOverflowError，可以使用迭代解决方案来替代递归：

// Recursion/Iteration.kt
package iteration
import atomictest.eq

fun sum(n: Long): Long {
  var accumulator = 0L
  for (i in 1..n) {
    accumulator += i
  }
  return accumulator
}

fun main() {
  sum(10000) eq 50005000
  sum(100000) eq 5000050000
}

这里没有 StackOverflowError 的风险，因为我们只进行了一次 sum() 调用，并且结果是在 for 循环中计算的。虽然迭代解决方案很简单，但必须使用可变状态变量 accumulator 来存储不断变化的值，而函数式编程试图避免变异。

为了防止调用栈溢出，函数式语言（包括 Kotlin）使用一种称为 尾递归 的技术。尾递归的目标是减小调用栈的大小。在 sum() 示例中，调用栈变为单个函数调用，就像在 Iteration.kt 中一样：

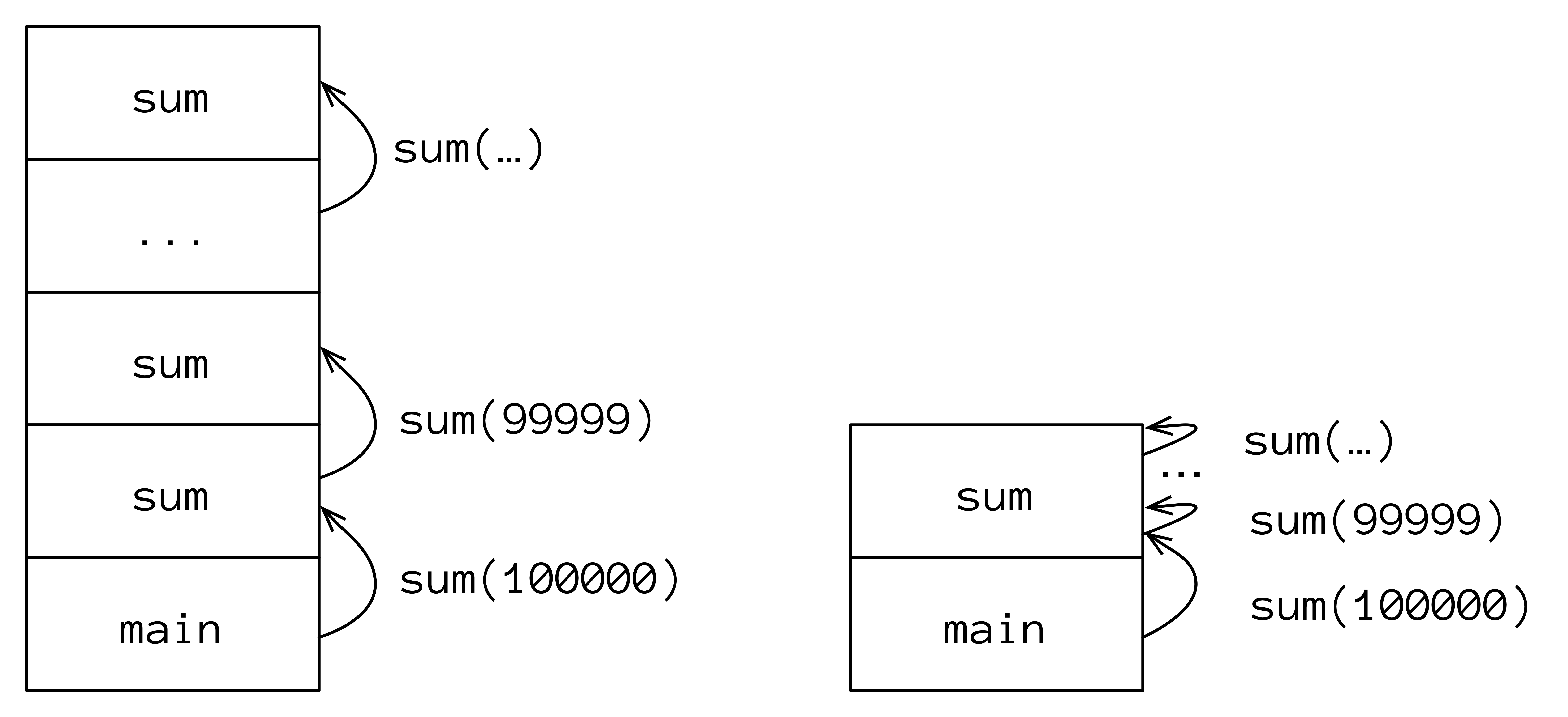
常规递归 vs. 尾递归

要产生尾递归，使用 tailrec 关键字。在正确的条件下，这会将递归调用转换为迭代，从而消除调用栈的开销。这是一个编译器优化，但不会对所有递归调用都有效。

要成功使用 tailrec，递归必须是最终操作，这意味着在返回之前不能对递归调用的结果进行任何额外的计算。例如，如果我们只是在 RecursionLimits.kt 中的 fun 前面放置了 tailrec，Kotlin 会生成以下警告消息：

• A function is marked as tail-recursive but no tail calls are found
• Recursive call is not a tail call

问题在于在返回结果之前将 n 与递归 sum() 调用的结果 结合 起来。为了使 tailrec 成功，递归调用的结果必须在返回时不进行任何处理。这通常需要对函数进行重新排列。对于 sum()，一个成功的 tailrec 如下所示：

// Recursion/TailRecursiveSum.kt
package tailrecursion
import atomictest.eq

private tailrec fun sum(
  n: Long,
  accumulator: Long
): Long =
  if (n == 0L) accumulator
  else sum(n - 1, accumulator + n)

fun sum(n: Long) = sum(n, 0)

fun main() {
  sum(2) eq 3
  sum(10000) eq 50005000
  sum(100000) eq 5000050000
}

通过包含 accumulator 参数，加法发生在递归调用期间，您在返回结果时不对其进行任何处理。现在，tailrec 关键字可以成功使用，因为代码已重写为将所有活动委托给递归调用。此外，accumulator 变为一个不可变值，消除了我们对 Iteration.kt 的抱怨。

factorial() 是一个常见的示例，用于演示尾递归，并且是本节的一个练习。另一个示例是斐波那契数列，其中每个新的斐波那契数是前两个数的和。前两个数字是 0 和 1，产生以下序列：0, 1, 1, 2, 3, 5, 8, 13, 21 ... 这可以递归地表示：

// Recursion/VerySlowFibonacci.kt
package slowfibonacci
import atomictest.eq

fun fibonacci(n: Long): Long {
  return when (n) {
    0L -> 0
    1L -> 1
    else ->
      fibonacci(n - 1) + fibonacci(n - 2)
  }
}

fun main() {
  fibonacci(0) eq 0
  fibonacci(22) eq 17711
  // 非常耗时：
  // fibonacci(50) eq 12586269025
}

这个实现非常低效，因为不会重用先前计算的结果。因此，操作数量呈指数级增长：

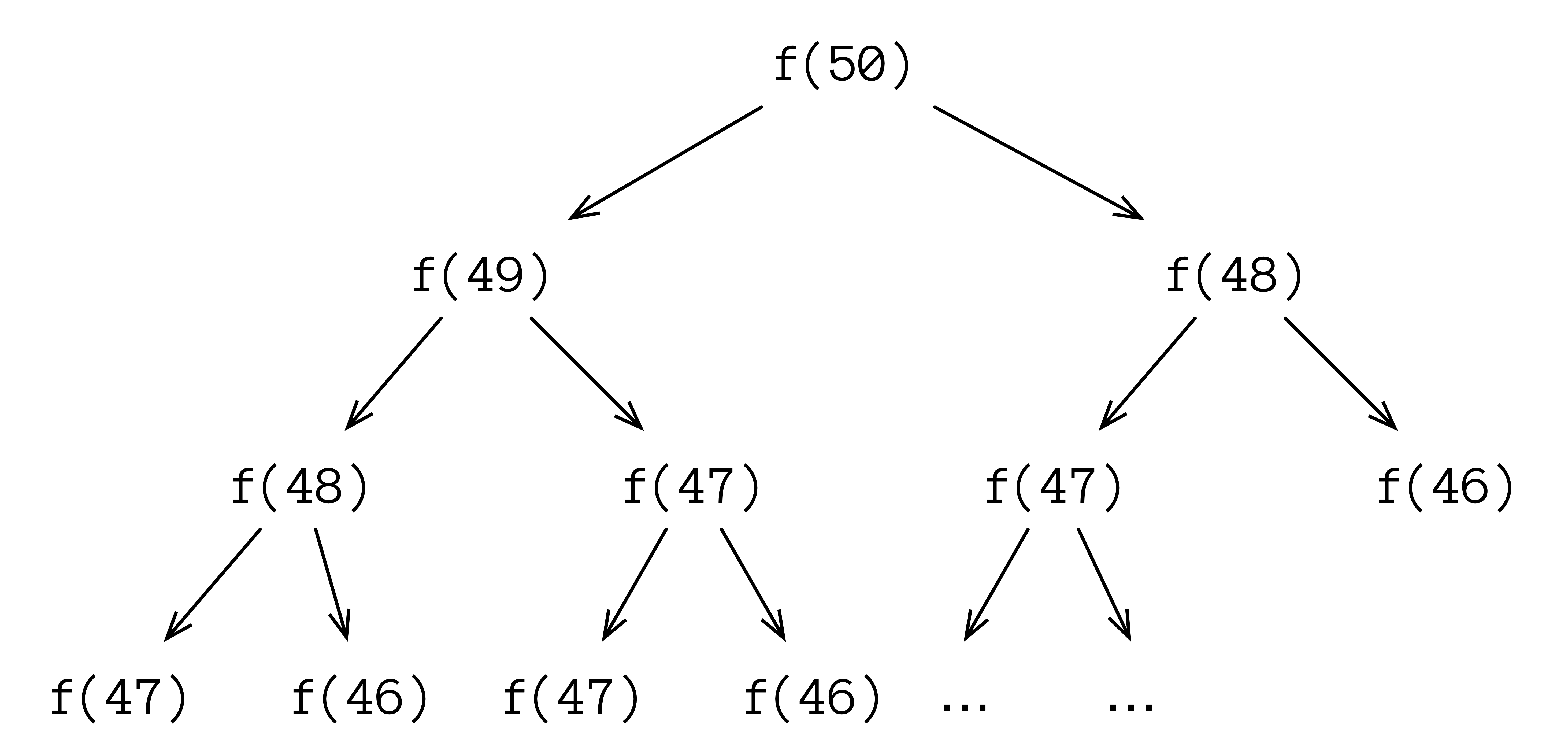
斐波那契数的低效计算

在计算第 50 个斐波那契数时，我们首先独立计算第 49 个和第 48 个数，这意味着我们计算第 48 个数两次。第 46 个数最多计算 4 次，依此类推。

使用尾递归，计算变得非常高效：

// Recursion/Fibonacci.kt
package recursion
import atomictest.eq

fun fibonacci(n: Int):

 Long {
  tailrec fun fibonacci(
    n: Int,
    current: Long,
    next: Long
  ): Long {
    if (n == 0) return current
    return fibonacci(
      n - 1, next, current + next)
  }
  return fibonacci(n, 0L, 1L)
}

fun main() {
  (0..8).map { fibonacci(it) } eq
    "[0, 1, 1, 2, 3, 5, 8, 13, 21]"
  fibonacci(22) eq 17711
  fibonacci(50) eq 12586269025
}

我们可以通过使用默认参数来避免本地的 fibonacci() 函数。但是，默认参数意味着用户可以将其他值放入这些默认值中，从而产生错误的结果。因为辅助的 fibonacci() 函数是一个局部函数，所以我们不会暴露额外的参数，您只能调用 fibonacci(n)。

main() 显示了斐波那契序列的前八个元素，结果为 22，最后是现在非常快速地产生的第 50 个斐波那契数。

练习和解答可以在 www.AtomicKotlin.com 找到。